浮点数在计算机中的表示

前言

相信大家在编程过程中都有使用过浮点数，但是浮点数总是给我带来预期不一样的结果，下面展示了在 C 语言中的精度问题，发现使用浮点数总是会带来精度缺失。在学习和工作当中总能听到不能使用浮点数来表示金钱，会有精度缺失。

#include <stdio.h>

int main() {
    float a = 0.1 + 0.2;
    printf("a = %.20f\n", a); // 0.30000001192092895508
    return 0;
}

但是在一些特殊领域，单靠整数是无法满足精度要求，这个时候就需要用到浮点数。这边篇文章来解释浮点数在计算机中是如何表示。

二进制小数

我们先类比一下比较熟悉的十进制数，比如 3.25 可以表示为：

3 * 10^0 + 2 * 10^-1 + 5 * 10^-2 = 3.25

如果我们只用 1 字节二进制来表示，一共 8 位，前 4 位表示整数，后 4 位表示小数，可以表示为0011 0100 ：

1 * 2^1 + 1 * 2^0 + 0 * 2^-1 + 1 * 2^-2 = 3.25

这种定点表示不能很有效的表示很大的数，我们一般在计算机中表示小数也不是使用这种方式，而是使用 IEEE 浮点表示方法。

IEEE 浮点数表示

IEEE 二进制浮点数算术标准（IEEE 754）是20世纪80运算标准，为许多CPU与浮点运算器所采用。这个标准定义了表示浮点数的格式包括负零（-0）与反常值（denormal number），一些特殊数值，比如无穷（Inf）与非数值（NaN），以及这些数值的“浮点数运算符”；它也指明了四种数值舍入规则和五种例外状况（包括例外发生的时机与处理方式）

IEEE 浮点数标准用如下 V = (-1)^s * M * 2^E 形式来表示一个数：

• 符号（sign）：s 决定这个数是负数（s = 1）还是正数（s = 0）
• 尾数（significand）：M 是一个二进制小数他的范围是 [1,2)
• 阶码（exponent）: E 的作用是对浮点数加权，这个权重是 2 的 E 次幂，也可以为负

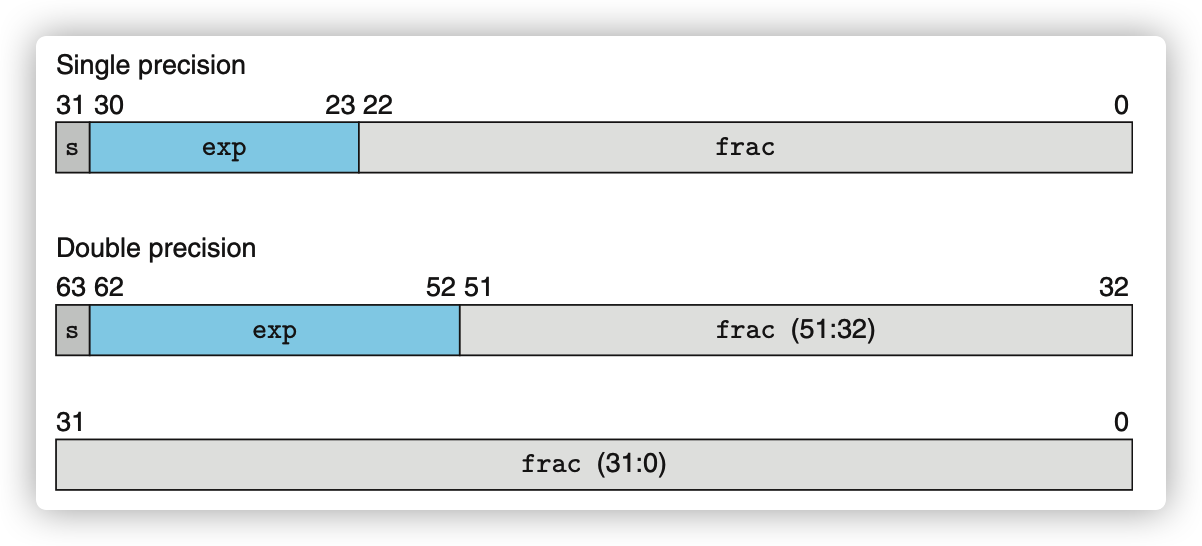
其中 s 对应着符号位，exp 对应着 E（注意，不一定等于 E，因为位数限制表达能力有限），frac 对应着 M（注意，不一定等于 M，因为位数限制表达能力有限）。不同的位数就代表了不同的表示能力，也就是单精度，双精度，扩展精度的来源。

给定表示，根据 exp 的值，被编码的值可以分成三种不同的情况，最后一种有两种不同的变种：

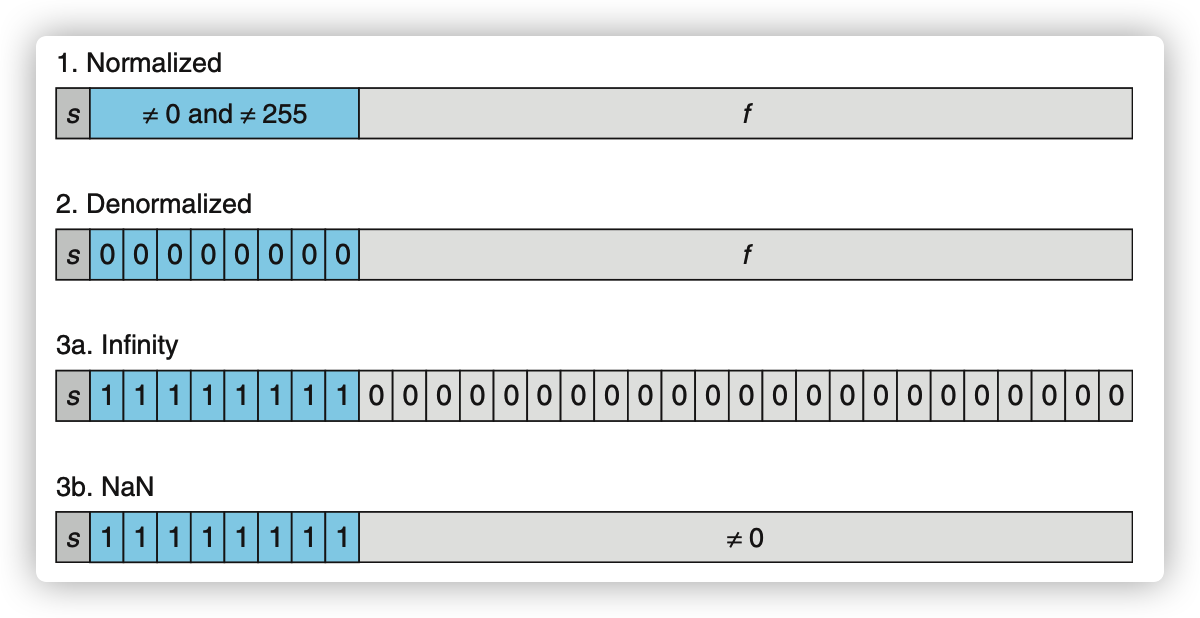
规范化值(Normalized Values)

当 exp 位不全为 0，也不全为 1，阶码的值 E = e - Bias ，其中 e 是无符号数（单精度取值范围 [1, 254] ），而 Bias 是一个等于 2^(k-1) - 1的偏置值（单精度为127）。所以 E 的取值范围为[-126, 127]。

小数字段 frac 被解释描述为 f 取值范围 [0, 1)，表示二进制小数点最高有效位。尾数定义为 M = 1 + f ，隐式表示。既然我们总能调整阶码 E，使得尾数的范围在 [1, 2) 范围中，那么这种表示方法就可以额外获取一个精度位技巧，既然第一位总是 1，那么我们就不需要显式地表现。

非规范化值(Denormalized Values)

当阶码域全为 0 时，所表示的数是非规格化形式。在这种情况下，阶码的值 E = 1 - Bias，而尾数的值 M = f 也就是小数字段，不包含隐式的开头 1。

为什么阶码的值为 1 - Bias 而不是 -Bias，这种方式提供了一种从非规格化值平滑转换的规格化值得一直手段。

非规格化有两个用途：

• 表示 0 ，当 f 全为 0 时，但是由于有符号位，则有 +0 和 -0 两种。
• 表示那些非常接近 0 的数。

特殊值

当阶码全为 1，而小数域全为 0 时，当符号位为 0 表示正无穷，当符号为 1，表示负无穷。

当小数域不全为 0 时，被称为 NaN （Not a Number），比如当计算根号一个负数，或者计算无穷减无穷。

具体表示

浮点数在坐标轴上的表示，接下来举一个实际的例子。

我们采用 1 位符号位，4 位 exp 位，3 位 frac 位，因此对应的 bias 为 7。

回顾前面公式，V = (-1)^s * M * 2^E，对于规范化数：E = exp − Bias ；对于非规范数：E = 1 − Bias。

这种形式的最小规格化同样有 E = 1 - 7 = -6 ，并且小数的取值范围也 0，1/8，…，7/8，发现最大规格化数 7/512 到最小规格化数 8/512 直接的平滑转变，这种平滑性归功于我们对非规格化数 E 的定义为 1 - Bias，而不是 -Bias，我们补偿非规格化的尾数没有隐含开头的 1。

最大规格数为 240，再增大就会溢出为正无穷。

例子

求 01000011110110000000110011001101 代表的浮点数？

s   exp           frac
1    8             23
0 10000111 10110000000110011001101

• E = exp - Bias = 135 - 127 = 8
• M = 1.10110000000110011001101
• V = (-1)^s * M * 2^E = 1 * 1.10110000000110011001101 * 2^8 = 110110000.000110011001101 = 432.10000620

求 123.4 的二进制表示？

s    exp          frac 
1    8             23
0 0000000 00000000000000000000

除 2            乘 2
123            0.4
 61 1          0.8  0
 30 1          0.6  1
 15 0          0.2  1
  7 1          0.4  0
  3 1          0.8  0
  1 1          0.6  1
  0 1          0.2  1

所以这个数为：01111011.01100110011001100110 = 01.11101101100110011001100110 * 2^6 
所以 E = 6 exp = 1110 1101 1001 1001 1001 100

• 因为 123.4 为正数，所以 s 为 0
• E = exp - Bias ，单精度 Bias 为 127，E 为 5，所以 exp = E + Bias = 6 + 127 = 133 = 1000 0101
• 结果为 0 10000101 11101101100110011001100

最后我们用 Java 程序来验证一下

public class BitTest {
    public static void main(String[] args) {
        printf(432.1f); 
        printf(123.4f); 

    }

    private static void printf(float f) {
        String s = Integer.toBinaryString(Float.floatToIntBits(f));
        StringBuilder zero = new StringBuilder();
        if (s.length() < 32) {
            int len = 32 - s.length();
            for (int i = 0; i < len; i++) {
                zero.append("0");
            }
        }
        String binary = zero.toString() + s;
        System.out.println(binary.substring(0, 1) + " " + binary.substring(1, 9) + " " + binary.substring(9, 32));
    }
}

输出结果

0 10000111 10110000000110011001101
0 10000101 11101101100110011001101

发现我我们前面所计算的相同，验证我们手动计算的正确性，通过这两个例子可以加深对浮点数表示的认识。

总结

本篇文章简单的介绍了 IEEE 浮点表示，介绍了规格化和非规格化的计算方式，以及如何从非规格化过度到规格化，通过通过这两个例子可以加深对浮点数表示的认识。虽然平时工作可能用不太到，但是当我看到这样设计觉得挺赞的，尤其是从非规格化到规格化的平滑过度。

参考

• 深入理解计算机系统
• 【读薄 CSAPP】壹 数据表示